Què és una equació?
Una equació és una igualtat entre dues expressions algebraiques. L’expressió de l’esquerra rep el nom de primer membre i l’equació de la dreta segon membre.
Dins d’una equació sempre hi trobem una o més incògnites, representades amb lletres (x, y o z ), el valor de la qual es desconeix fins a trobar la solució, és a dir, el valor numèric de la incògnita.
Una equació de primer grau és aquella que té només una incògnita i l’exponent és 1 (no està elevat al quadrat, al cub…)

Passos per resoldre una equació de primer grau
Resoldre una equació de primer grau vol dir trobar el valor que s’amaga darrere la incògnita x. Llavors, l’objectiu és aïllar la x, simplificant al màxim l’equació per saber quin nombre representa x.
Per fer-ho, s’han de tenir clares dues normes a l’hora de canviar els termes a diferents costats de l’equació:
- Quan un terme que està sumant o restant a un altre terme passa a l’altre membre (costat de l’equació), el seu signe s’inverteix (si era positiu passa a negatiu i a la inversa)
- Quan un terme està multiplicant la incògnita, passa a l’altre membre dividint i a la inversa, si estava dividint passa multiplicant.
Tenint en compte aquestes normes, els passos a seguir per resoldre una equació de primer grau són els següents:

1.Es passen tots els termes que tenen incògnita (x) a un membre (normalment al costat esquerre) i els termes sense incògnita a l’altre membre (costat dret) tenint en compte el canvi de signe.

2. S’efectuen les sumes i restes que pertoquin fins que només quedi un terme a cada costat.
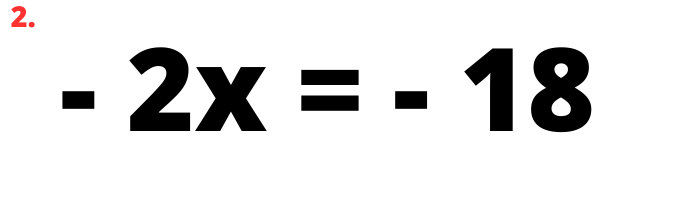
3. Si hi ha un terme multiplicant la incògnita (x), aquest passa a l’altre membre invertint la seva operació, és a dir dividint.

4. Resoldre l’equació.
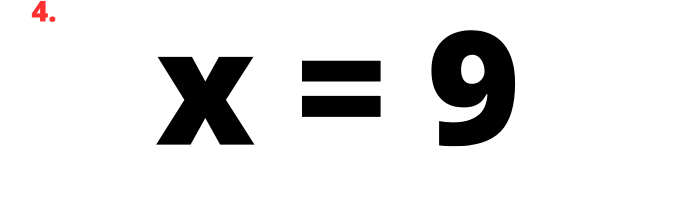
5. Comprovar el resultat. Una vegada es coneix el valor de x, es pot substituir x a l’equació inicial pel valor que s’ha obtingut. Si l’equació es compleix, és a dir que a cada costat de l’equació s’obté el mateix resultat, significa que el valor de x és el correcte i que l’equació ha estat resolta satisfactòriament.
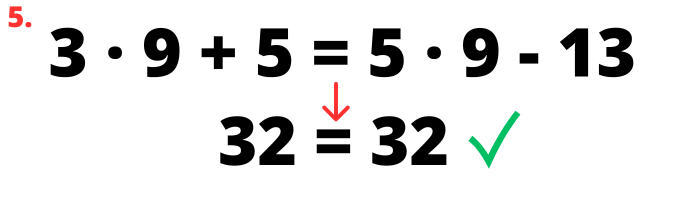
En aquest exemple, l’equació era senzilla, tot i això, el procediment és sempre el mateix, encara que en altres casos s’hauran d’efectuar més operacions prèviament.
En aquest vídeo podeu observar el mètode explicat i exemples amb més dificultat per poder practicar. Endavant!


Hola Maria Antonia, crec que lo dol valor de la ”x” ho he entes bastan bé,sols que en el minut onze i vint-i-cinc ja no he entes res. Si és que el Dimecres tractam aquest tema m’agradaria que m’ho expliquis.